Como estoy muy interesado en la situación educativa española (el que me conozca conocerá la razón), siempre que se pone a tiro un artículo sobre el tema lo leo sin rechistar. El artículo siguiente me ha parecido muy interesante y coincide con lo que pienso del tema, es decir, resumiendo:
- La culpa es de los padres.
- Los alumnos son vagos y maleducados, cuando no directamente cuasidelincuentes.
- La política de igualar el nivel por abajo no puede ser más perjudicial.
- De la misma forma que los alumnos tienen derecho a la educación, también tienen obligaciones: la obligación de aprovechar los recursos que se ponen a su disposición con el dinero de todos. Esto se lo escuché al juez Emilio Calatayud.
- El profesor es el primer interesado en que las clases se desarrollen con normalidad, a salvo de continuas interrupciones, insultos, peleas o gamberradas. Si los profesores quisieran ser policías no hubieran escogido esta profesión.
Os recomiendo su lectura: El verdadero problema de la educación en España
De las nuevas ideas del artículo me quedo con que antes que el "plan de calidad" del profesorado (no es más una forma de evaluar a un profesor según el número de aprobados), habría que crear el plan de seguimiento para los padres, para que no pasaran de sus hijos.
viernes, 24 de abril de 2009
sábado, 18 de abril de 2009
La curva de Laffer
Hace unos días en "59 segundos" dedicaron el programa a hablar de la crisis. Entre los invitados estuvo Cristobal Montoro (portavoz en asuntos ecómicos PP) que nombró en varias ocasiones la bajada de impuestos como una buena medida para luchar contra la crisis. Celestino Corbacho, ministro de Inmigración y Trabajo, no compartió la opinión defendiendo que esto generaría una menor recaudación. Recordemos que el estado está endeudándose actualmente en un intento por animar a la economía y precisamente no es éste un buen momento para recaudar menos.
Por supuesto que el ministro tiene razón, pero no toda, ya que una bajada de impuestos proporcionaría una mayor renta a los ciudadanos que podrían así aumentar su consumo, generando una mayor producción, incrementando el empleo y en definitiva mayor número de personas pagarían impuestos que de forma global generaría una mayor recaudación que anteriormente.
Arthur B. Laffer fue un economista que hace ya mucho tiempo se dio cuenta que una subida de impuestos puede tener como resultado dos escenarios distintos: uno de menor recaudación y otra de mayor. Este pensamiendo lo modeló en una representación gráfica que tomó el nombre de Curva de Laffer:
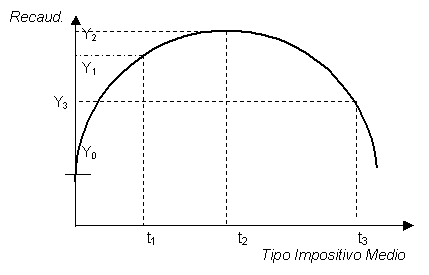En la curva vemos que el eje horizontal (X) representa el tipo impositivo (cuanto más a la derecha, mayores impuestos).
En el eje vertical (Y) se representa la recaución estatal (cuanto más arriba, más altos serán los impuestos).
Partiendo del tipo de impositivo t1, vemos que aún se pueden subir los impuestos aumentando la recaudación. Sin embargo si se sobrepasa el tipo impositivo t2 se consigue el efecto contrario, disminuyendo la recaudación.
Por supuesto que el ministro tiene razón, pero no toda, ya que una bajada de impuestos proporcionaría una mayor renta a los ciudadanos que podrían así aumentar su consumo, generando una mayor producción, incrementando el empleo y en definitiva mayor número de personas pagarían impuestos que de forma global generaría una mayor recaudación que anteriormente.
Arthur B. Laffer fue un economista que hace ya mucho tiempo se dio cuenta que una subida de impuestos puede tener como resultado dos escenarios distintos: uno de menor recaudación y otra de mayor. Este pensamiendo lo modeló en una representación gráfica que tomó el nombre de Curva de Laffer:
En la curva vemos que el eje horizontal (X) representa el tipo impositivo (cuanto más a la derecha, mayores impuestos).En el eje vertical (Y) se representa la recaución estatal (cuanto más arriba, más altos serán los impuestos).
Partiendo del tipo de impositivo t1, vemos que aún se pueden subir los impuestos aumentando la recaudación. Sin embargo si se sobrepasa el tipo impositivo t2 se consigue el efecto contrario, disminuyendo la recaudación.
Resolución de ecuaciones
Mediante la página PHPSimplex podremos resolver problemas de optimización con ecuaciones e inecuaciones y varias incógnitas usando el método Simplex, es decir, problemas de Investigación Operativa.
En el caso de usar 2 incógnitas podremos resolver el problema gráficamente, que siempre es más instructivo.
Vamos a intentar resolver un problema típico de gestión de la producción. Supongamos que tenemos una pequeña fábrica que puede fabricar motos (X1) y bicicletas (X2) y queremos planificar la producción para un periodo de tiempo. Con cada moto vendida tenemos un beneficio de 500 euros, mientras que por cada bicicleta tenemos un beneficio de 100 euros. Las restricciones que tenemos son:
- Solamente disponemos de 100.000 euros para invertir en la fabricación de los productos. Fabricar una moto nos cuesta 3000 euros y fabricar una bici nos cuenta 200 euros.
- Como estamos empezando y tenemos poco espacio, no podemos fabricar más de 20 motos.
Una vez leído el enunciado del problema tenemos que modelar el problema:
- Incógnitas: X1 (número de motos fabricadas), X2 (número de bicicletas fabricadas)
- Función objetivo: Es la relación entre las incógnitas que queremos maximizar o minimizar. En nuestro caso queremos maximizar los beneficios. Recordemos que por cada moto obtenemos un beneficio de 500 euros y de 100 por cada bici. Así pues, queremos maximizar:
Max: 500X1 + 100X2
- Restricciones: Son varias:
1) Límite presupuestario teniendo en cuenta lo que cuesta cada producto en fabricar:
3000X1 + 200X2 <= 100000
2) Límite de espacio. No podemos fabricar más de 20 motos: X1<=20
El siguiente paso es pasar el modelo creado a PHPSimplex :
1) Introduccimos:
Método: Gráfico
Nº incógnitas: 2
Nº restricciones: 2
2) Introduccimos:
Objetivo de la función: Maximizar
Función: 500X1 + 100X2
Restricción:
3000X1 + 200X2 <= 100000
X1<=20
El resultado es el siguiente:
Luego si fabricamos 500 bicicletas conseguiremos maximizar nuestros beneficios (50.000 euros).
En el caso de usar 2 incógnitas podremos resolver el problema gráficamente, que siempre es más instructivo.
Vamos a intentar resolver un problema típico de gestión de la producción. Supongamos que tenemos una pequeña fábrica que puede fabricar motos (X1) y bicicletas (X2) y queremos planificar la producción para un periodo de tiempo. Con cada moto vendida tenemos un beneficio de 500 euros, mientras que por cada bicicleta tenemos un beneficio de 100 euros. Las restricciones que tenemos son:
- Solamente disponemos de 100.000 euros para invertir en la fabricación de los productos. Fabricar una moto nos cuesta 3000 euros y fabricar una bici nos cuenta 200 euros.
- Como estamos empezando y tenemos poco espacio, no podemos fabricar más de 20 motos.
Una vez leído el enunciado del problema tenemos que modelar el problema:
- Incógnitas: X1 (número de motos fabricadas), X2 (número de bicicletas fabricadas)
- Función objetivo: Es la relación entre las incógnitas que queremos maximizar o minimizar. En nuestro caso queremos maximizar los beneficios. Recordemos que por cada moto obtenemos un beneficio de 500 euros y de 100 por cada bici. Así pues, queremos maximizar:
Max: 500X1 + 100X2
- Restricciones: Son varias:
1) Límite presupuestario teniendo en cuenta lo que cuesta cada producto en fabricar:
3000X1 + 200X2 <= 100000
2) Límite de espacio. No podemos fabricar más de 20 motos: X1<=20
El siguiente paso es pasar el modelo creado a PHPSimplex :
1) Introduccimos:
Método: Gráfico
Nº incógnitas: 2
Nº restricciones: 2
2) Introduccimos:
Objetivo de la función: Maximizar
Función: 500X1 + 100X2
Restricción:
3000X1 + 200X2 <= 100000
X1<=20
El resultado es el siguiente:
Luego si fabricamos 500 bicicletas conseguiremos maximizar nuestros beneficios (50.000 euros).
viernes, 17 de abril de 2009
Mapas de Europa entre los años 0 al 2000
En Euroatlas se pueden ver mapas de Europa entre los años 0 y 2000. En ellos podemos ver los reinos/paises/califatos que la han ocupado a lo largo de la historia. Muy interesante.
miércoles, 15 de abril de 2009
La ocasión la pintan calva
Todos conocemos que "la ocasión la pintan calva" significa que es una buena oportunidad y que no la debemos dejar escapar.
El origen de esta frase la encontramos en la diosa Ocasión (compañera de la diosa Fortuna). La diosa Ocasión tenía la cabeza rapada por la parte de atrás, de manera que si se la dejaba pasar de largo ya no se la podía agarrar del pelo porque era calva.
A la diosa se la representa sobre una rueda para indicar que nunca está quieta y tiene un cuchillo para mostrar lo rápida que es, tanto que "corta el aire".
Así que ya sabes, cuando tengas una buena oportunidad agárrala porque quizás luego ya sea tarde.
lunes, 13 de abril de 2009
E=mc^2: Biografía de la ecuación más famosa de Einstein
Durante la Semana Santa he podido terminar el libro que tenía entre manos: "E=mc^2: Biografía de la ecuación más famosa de Einstein" de David Bodanis.Todos conocemos esta ecuación aunque seguro que sólo una parte conoce lo que realmente significa y lo que significó para el desarrollo de la Humanidad. Descubrir lo que hubo y hay detrás de esta ecuación es lo que se propuso el autor
Cuando pensamos en un genio, seguramente muchos pensemos en Albert Einstein, aunque éste al parecer era un poco patoso y no era considerado como un buen estudiante, siendo reprendido por sus profesores por no respetar las normas.
La famosa ecuación E=mc^2 relaciona varios elementos, veámoslo:
- E: Energía
- m: Masa
- c : Velocidad de la luz, es decir, 300.000 Km/s en el vacío.
Einstein predijo que toda masa tiene una energía asociada y ésta es directamente proporcional a la velocidad de la luz. Este resultado fue teórico, ya que Einstein no fue capaz de demostrarlo.
Tiempo después se consiguió realizar la fisión nuclear, es decir, la partición de un núcleo (de uranio por ejemplo) por el lanzamiento de neutrones y la liberación de energía. Se cumple que la masa de las dos mitades es menor a la masa inicial, por lo que se produce una pérdida de masa. Resulta que la energía liberada es igual a E=mc^2, siendo m la masa desaparecida. Se había demostrado que la ecuación de Einstein era cierta.
Ante la visión de que su ecuación podía usarse con fines bélicos (como posteriormente se demostró con la bomba atómica), Einstein envió la siguiente carta al presidente estadounidense Roosevelt:
Algunos trabajos recientes [...], que me han sido comunicados en forma manuscrita, me hacen suponer que el uranio se convertirá en una nueva e importante fuente de energía en un futuro inmediato. Ciertos aspectos de la situación que se ha creado parecen exigir vigilancia, y si fuera necesario una rápida acción por parte de la Administración.
Este nuevo fenómeno puede [...] llevar a la construcción de bombas, y es concedible -aunque mucho menos seguro- que se puedan fabricar explosivos extremadamente poderosos de un nuevo tipo. Una sola bomba de ese estilo, transportada en un barco y a la que se hiciera explotar en un puerto, podría hacerlo desaparecer por entero, y con él buena parte del territorio circundante [...].
Además de la bomba atómica, las explosiones que ocurren en el Sol también se pueden explicar con esta ecuación. En el Sol se produce la fusión de átomos de hidrógeno en átomos de helio, haciendo desaparecer masa como anteriormente y ... liberando energía según la ecuación de Einstein. Así pues queda claro que cada vez que desaparezca o se desintegre masa tendremos energía. Si te preguntas cuánto tiempo más el Sol podrá producir energía, aquí tienes una posible cifra.
Respecto a la velocidad de la luz se cuenta una anécdota muy curiosa. Supongamos que estamos en un bar y en una mesa cercana hay una mujer hablando por teléfono con otra persona que se encuentra en la otra punta del mundo. Se da la curiosa circunstancia de que el otro interlocutor en la charla telefónica está escuchando antes que nosotros lo que la mujer dice por teléfono, aún estando nosotros a unos escasos metros. La explicación se debe a que el sonido por el teléfono se mueve mediante ondas de radio por lo que que se mueven a la velocidad de la luz, mientras que nosotros estamos escuchando las ondas de radio que se mueven a la velocidad del sonido, es decir 340 m/s.
La velocidad de la luz es la velocidad más rápida a la que se puede mover un objeto, de la misma manera que -273ºC es la mínima temperatura o cero absoluto.
Las aplicaciones de la famosa ecuación son más cercanas que fusiones y fisiones. Por ejemplo:
1) Luces de emergencia en los cines. No tiene sentido que una luz de emergencia esté alimentada por la electricidad de un edificio, porque si sucede algo, la luz de emergencia no se encenderá o no cumplirá su objetivo. Realmente las luces de emergencia contienen una pequeña cantidad de tritio, parte de cuya masa se va "perdiendo" o desintegrando constantemente, por lo que usando la famosa ecuación sabemos que se está produciendo energía que se utiliza para producir la luz.
2) Escáneres TEP (Topografía mediante Emisión de Positrones). En este caso el paciente respira un isótopo radiactivo del oxígeno que tras desintegrarse en el interior del cuerpo genera una energía que es monitorizada desde el exterior.
3) Radioterapia. En este caso se lanza cobalto radiactivo sobre el tumor y tras su desintegración genera energía que mata el ADN canceroso.
Mi calificación: 7
La famosa ecuación E=mc^2 relaciona varios elementos, veámoslo:
- E: Energía
- m: Masa
- c : Velocidad de la luz, es decir, 300.000 Km/s en el vacío.
Einstein predijo que toda masa tiene una energía asociada y ésta es directamente proporcional a la velocidad de la luz. Este resultado fue teórico, ya que Einstein no fue capaz de demostrarlo.
Tiempo después se consiguió realizar la fisión nuclear, es decir, la partición de un núcleo (de uranio por ejemplo) por el lanzamiento de neutrones y la liberación de energía. Se cumple que la masa de las dos mitades es menor a la masa inicial, por lo que se produce una pérdida de masa. Resulta que la energía liberada es igual a E=mc^2, siendo m la masa desaparecida. Se había demostrado que la ecuación de Einstein era cierta.
Ante la visión de que su ecuación podía usarse con fines bélicos (como posteriormente se demostró con la bomba atómica), Einstein envió la siguiente carta al presidente estadounidense Roosevelt:
Algunos trabajos recientes [...], que me han sido comunicados en forma manuscrita, me hacen suponer que el uranio se convertirá en una nueva e importante fuente de energía en un futuro inmediato. Ciertos aspectos de la situación que se ha creado parecen exigir vigilancia, y si fuera necesario una rápida acción por parte de la Administración.
Este nuevo fenómeno puede [...] llevar a la construcción de bombas, y es concedible -aunque mucho menos seguro- que se puedan fabricar explosivos extremadamente poderosos de un nuevo tipo. Una sola bomba de ese estilo, transportada en un barco y a la que se hiciera explotar en un puerto, podría hacerlo desaparecer por entero, y con él buena parte del territorio circundante [...].
Además de la bomba atómica, las explosiones que ocurren en el Sol también se pueden explicar con esta ecuación. En el Sol se produce la fusión de átomos de hidrógeno en átomos de helio, haciendo desaparecer masa como anteriormente y ... liberando energía según la ecuación de Einstein. Así pues queda claro que cada vez que desaparezca o se desintegre masa tendremos energía. Si te preguntas cuánto tiempo más el Sol podrá producir energía, aquí tienes una posible cifra.
Respecto a la velocidad de la luz se cuenta una anécdota muy curiosa. Supongamos que estamos en un bar y en una mesa cercana hay una mujer hablando por teléfono con otra persona que se encuentra en la otra punta del mundo. Se da la curiosa circunstancia de que el otro interlocutor en la charla telefónica está escuchando antes que nosotros lo que la mujer dice por teléfono, aún estando nosotros a unos escasos metros. La explicación se debe a que el sonido por el teléfono se mueve mediante ondas de radio por lo que que se mueven a la velocidad de la luz, mientras que nosotros estamos escuchando las ondas de radio que se mueven a la velocidad del sonido, es decir 340 m/s.
La velocidad de la luz es la velocidad más rápida a la que se puede mover un objeto, de la misma manera que -273ºC es la mínima temperatura o cero absoluto.
Las aplicaciones de la famosa ecuación son más cercanas que fusiones y fisiones. Por ejemplo:
1) Luces de emergencia en los cines. No tiene sentido que una luz de emergencia esté alimentada por la electricidad de un edificio, porque si sucede algo, la luz de emergencia no se encenderá o no cumplirá su objetivo. Realmente las luces de emergencia contienen una pequeña cantidad de tritio, parte de cuya masa se va "perdiendo" o desintegrando constantemente, por lo que usando la famosa ecuación sabemos que se está produciendo energía que se utiliza para producir la luz.
2) Escáneres TEP (Topografía mediante Emisión de Positrones). En este caso el paciente respira un isótopo radiactivo del oxígeno que tras desintegrarse en el interior del cuerpo genera una energía que es monitorizada desde el exterior.
3) Radioterapia. En este caso se lanza cobalto radiactivo sobre el tumor y tras su desintegración genera energía que mata el ADN canceroso.
Mi calificación: 7
domingo, 12 de abril de 2009
Portable Ubuntu
Esta mañana he estado probando la versión portable de Ubuntu. Para el que no lo conozca, Ubuntu es un sistema operativo basado en Linux, totalmente gratuito y que está muy de moda.
Hasta ahora existían versiones instalables y cd-lives (arrancable desde cd sin necesidad de instalación), pero no versiones portables. Lo bueno de las versiones portables es que no necesitan instalación ni reiniciar el sistema, simplemente se ejecutan y ya está.
Para poder probarla tendremos que:
1. Descargar Portable Ubuntu.
2. Descomprimir el contenido del archivo. Para ello basta con ejecutar el archivo bajado y guardarlo en alguna carpeta.
3. Abrir una consola del sistema como administrador. Para ello:
- Ir a la opción "Programas/ Accesorios"
- Colocarnos sobre "Símbolo del sistema", pulsar con el botón derecho y seleccionamos "Ejecutar como Administrador".
4. Navegar hasta donde hayamos descomprimido en el paso 2. Por ejemplo "cd \users\yo\desktop\portable_desktop".
5. Ejecutar "run_portable_ubuntu.bat".
Tras esto se nos abrirá una pequeña ventanita en forma de menú desde el que podremos ejecutar las aplicaciones de Ubuntu.
Si os habéis perdido con tantos pasos, aquí tenéis un vídeo (en inglés, aunque lo importante es ver cómo se hace) que hace lo mismo:
Hasta ahora existían versiones instalables y cd-lives (arrancable desde cd sin necesidad de instalación), pero no versiones portables. Lo bueno de las versiones portables es que no necesitan instalación ni reiniciar el sistema, simplemente se ejecutan y ya está.
Para poder probarla tendremos que:
1. Descargar Portable Ubuntu.
2. Descomprimir el contenido del archivo. Para ello basta con ejecutar el archivo bajado y guardarlo en alguna carpeta.
3. Abrir una consola del sistema como administrador. Para ello:
- Ir a la opción "Programas/ Accesorios"
- Colocarnos sobre "Símbolo del sistema", pulsar con el botón derecho y seleccionamos "Ejecutar como Administrador".
4. Navegar hasta donde hayamos descomprimido en el paso 2. Por ejemplo "cd \users\yo\desktop\portable_desktop".
5. Ejecutar "run_portable_ubuntu.bat".
Tras esto se nos abrirá una pequeña ventanita en forma de menú desde el que podremos ejecutar las aplicaciones de Ubuntu.
Si os habéis perdido con tantos pasos, aquí tenéis un vídeo (en inglés, aunque lo importante es ver cómo se hace) que hace lo mismo:
jueves, 9 de abril de 2009
Perfect Balance
Perfect Balance es un juego en el que tenemos que colocar piezas de manera que consigan estar en equilibrio y no caigan al suelo.
La forma de jugar es la siguiente:
- Seleccionar el nivel en el menú principal, por ejemplo "Harmony".
- Hacer click sobre la pieza que queremos utilizar y llevarla donde deseamos colocarla, girándola si es necesario.
- Hacer click para "liberar" la pieza.
- Colocar el resto de piezas.
- Si hemos conseguido el "equilibrio perfecto", pasaremos al siguiente nivel.
Las teclas que nos hará falta utilizar son:
- R : Comenzar
- A, D : Rotar piezas
La forma de jugar es la siguiente:
- Seleccionar el nivel en el menú principal, por ejemplo "Harmony".
- Hacer click sobre la pieza que queremos utilizar y llevarla donde deseamos colocarla, girándola si es necesario.
- Hacer click para "liberar" la pieza.
- Colocar el resto de piezas.
- Si hemos conseguido el "equilibrio perfecto", pasaremos al siguiente nivel.
Las teclas que nos hará falta utilizar son:
- R : Comenzar
- A, D : Rotar piezas
miércoles, 8 de abril de 2009
¿Para qué necesitamos ADSL a no sé cuántos gigas?
La recién estrenada Ministra de Cultura González-Sinde pronunció unas palabras que me han dejado totalmente anonadado. El tema en cuestión es que la Sra. Ministra se ha preguntado "¿Para qué necesitamos ADSL a no sé cuántos gigas? ¿Para mandar e-mails?"
Es decir que mientras que Japón incrementa la velocidad de su banda ancha a 1 giga, aquí la ministra quiere que nos quedemos en los 56Kb, que para mandar un e-mail es suficiente. Esto sí que es progreso, I+D, productividad, ...
Es decir que mientras que Japón incrementa la velocidad de su banda ancha a 1 giga, aquí la ministra quiere que nos quedemos en los 56Kb, que para mandar un e-mail es suficiente. Esto sí que es progreso, I+D, productividad, ...
La ministra se escuda en que Internet se utiliza en un alto porcentaje para la descarga de archivos ilegales. Ya puestos ha prohibir, podríamos que cerrar los puertos por si acaso introducen droga escondida, o apagar las televisiones para que no muestren violencia, o encarcelar a los políticos por si se quedan con dinero público, etc.
Con el tema del canon digital ya somos tratados culpables por definición. No vale que jures y perjures que los DVDs que compras son para grabar las fotos de tu último viaje, tendrás que pagar por si las moscas lo usas para grabar obras protegidas por copyright.
Y ya como pongan la excusa de que el cine español está en caída libre es por culpa del pirateo es que tiro al suelo a me harto a reir. No hay más ciego que el que no quiere ver. Mira como las películas españolas que merecen la pena sí que llenan las salas.
Vamos a intentar hacer una lista de tareas legales que podemos hacer en Internet gracias a la banda ancha y que sin ella no podríamos o sería demasiado lento:
- Ver televisión online. Por ejemplo la Televisión Pública Española.
- Escuchar radio online. Por ejemplo Sevilla Fútbol Club Radio.
- Ver vídeos. Ver el último video musical en Youtube de mi grupo favorito y comprármelo si me gusta en iTunes.
- Compra/visionado de películas.
- Intercambio de archivos con programas P2P. Por ejemplo bajarme los apuntes de una asignatura que se me resiste.
- Juegos online.
- Videoconferencias.
- Teléfono por internet. Por ejemplo: Skype
Internet abre un nuevo mercado en nuestra forma de vivir de igual forma que la imprenta, la radio o el teléfono la cambió en su momento. Quien no lo quiera aprovechar será desplazado del mercado.
martes, 7 de abril de 2009
¿Es necesaria la energía nuclear?
En los últimos tiempos estamos viviendo el boom de las energías renovables. Tanto es así que por fin estamos a la cabeza en algo bueno en España. Sin embargo no todo va a ser de color de rosa ya que se avisa que debemos de tener cuidado no vaya a ser que se conviertan las energías renovables en la nueva burbuja (ya tenemos bastante con la inmobiliaria).
La energía nuclear como todo tiene sus pros y sus contras. Entre sus pros se encuentran:
- En su generación no se utilizan combustibles fósiles, por lo que es limpia.
- Existe un algo control de las centrales nucleares.
- Es una forma de eliminar la dependencia energética de terceros.
- Es una energía "barata".
Entre sus contras se encuentran:
- Actualmente no existen mecanismos para eliminar los residuos radiactivos generados.
- En caso de fallo grave de la central, se repetiría otro "caso Chernobil". Aunque actualmente son muchas las medidas de seguridad, nunca se puede estar seguro.
También está el que está a favor de la energía nuclear siempre y cuando las energías renovables no estén lo suficientemente desarrolladas para ser rentables sin necesidad de subvenciones.
lunes, 6 de abril de 2009
Semana Santa 2009 online en Sevilla
Para el que no pueda ver en directo la Semana Santa de Sevilla, este año desde la página de Turismo Sevilla se puede ver el canal Giralda Tv Digital que realiza un seguimiento completísimo.
Almacenamiento de energía
Uno de los problemas existentes en la producción de energía es que una vez que se genera y no se consume, normalmente se pierde. Al parecer es caro e ineficiente intentar aprovechar esa energía por lo que se decide directamente perderla.
En el caso de la energía eléctrica existen curvas de demanda, de manera que para cada día se dispone de una previsión del consumo que se va a producir. Si el consumo aumenta, inmediatamente se pone en marcha alguna central extra.
Aún existiendo estas previsiones, la cantidad de energía producida siempre será mayor a la que se espera se consuma. Esta energía excedente que se produce se pierde, ya que aunque se puede aprovechar es caro hacerlo.
En este interesante artículo podéis conocer algunas de las alternativas que existen actualmente.
En el caso de la energía eléctrica existen curvas de demanda, de manera que para cada día se dispone de una previsión del consumo que se va a producir. Si el consumo aumenta, inmediatamente se pone en marcha alguna central extra.
Aún existiendo estas previsiones, la cantidad de energía producida siempre será mayor a la que se espera se consuma. Esta energía excedente que se produce se pierde, ya que aunque se puede aprovechar es caro hacerlo.
En este interesante artículo podéis conocer algunas de las alternativas que existen actualmente.
viernes, 3 de abril de 2009
El economista camuflado
Hace ya tiempo que leí "El Economisma camuflado" de Tim Harford, pero he ido procrastinando su presentación en el blog y ya por fín hoy sale de la horno.
Es un libro de fácil lectura que nos presenta diferentes asuntos y el autor los analiza desde el punto de vista de un economista. No es para nada un libro técnico. Veamos algunos de los asuntos tratamos:
1) La escasez. En este caso se nos presenta como la escasez (en este caso un local en una calle transitada) proporciona una fuerza grande en la negociación debido a que el recurso escaso proporciona un beneficio extra respecto a otro no tan escaso.
Hay ocasiones en la que la escasez se crea de forma artificial, por ejemplo en Londres existe un cinturón verde alrededor de la ciudad en el que por supuesto no hay viviendas sino parques, por lo que provoca que los barrios residenciales se encuentren muy alejados en distancia al centro de la ciudad. Esto crea una escasez de viviendas en el centro por lo que su precio es mayor respecto a las viviendas más allá del cinturón verde.
2) Información asimétrica. En un acuerdo si uno de los negociadores tiene más información que el otro, el acuerdo alcanzado no es "justo". Si ambas partes tuvieran la misma información el acuerdo no se llevaría a cabo o al menos no en las mismas condiciones.
3) Países pobres. Los países pobres deberían crecer más rápidamente que los ricos. Por ejemplo, la construcción de una simple carretera en un país pobre generará más beneficios en un país pobre que en uno rico.
Los países pobres tienen una carencia importancia en formación y tecnología, aunque quizás la mayor carencia sea que gran parte de las ayudas recibidas no llegan a materializarse por la corrupción galopante.
Mi calificación: 7
jueves, 2 de abril de 2009
El Enigma de Fermat
Ya he acabado con "El Enigma de Fermat" de Simon Singh, en el que se cuenta cómo Andrew Wiles consiguió demostrar el último Teorema de Fermat en el año 1995. 350 años después se conseguía demostrar tras haber sido intentado por innumerables matemáticos.
¿Cuál es el último Teorema de Fermat? La historia de este teorema está muy ligada a Pitágoras y su famosa fórmula sobre los triángulos rectángulos (la de los catetos y la hipotenusa):
c2 = a2 + b2
Se cuenta que mientras Fermat estudiaba el libro Arithmetica de Diofanto escribió en un margen del mismo:
Es imposible dividir un cubo en suma de dos cubos, o un bicuadrado en suma de dos bicuadrados, o en general, cualquier potencia superior a dos en dos potencias del mismo grado; he descubierto una demostración maravillosa de esta afirmación. Pero este margen es demasiado angosto para contenerla.
Es decir, para cualquier "n" mayor a 2 la siguiente ecuación no tiene solución para números enteros.
cn = an + bn
Para su resolución se necesitó que muchos matemáticos dieran pequeños pasitos, creando nuevas matemáticas, basándose unos en otros, pero teniendo todos el mismo resultado. Algunos de los grandes matemáticos que pusiereon su granito de arena fueron: Euler, Galois, Germain,
Se consiguieron demostrar casos, por ejemplo Euler para n=3 o Lamé para n=7, pero la demostración que vale, la demostración para todos los casos, no se conseguía alcanzar.
Es curioso que Andrew Wiles no tuvo que demostrar el teorema en sí, sino que tuvo que demostrar la conjetura de Taniyama-Shimura, ya que anteriormente se había demostrado que si esta conjeruta fuese cierta se demostraría la validez del Teorema de Fermat.
El libro no presenta una explicación técnica del Teorema, aunque en ocasiones se haga alguna referencia a fórmulas y demás, es más bien un repaso de los distintos matemáticos que lo han intentado resolver o que significaron algo en la vida de Andrew Wiles.
Mi calificación: 7
Como extra, aquí se puede ver el documental "El último teorema de Fermat" de la BBC Horizon.
Como extra, aquí se puede ver el documental "El último teorema de Fermat" de la BBC Horizon.
Suscribirse a:
Entradas (Atom)